Introduction

We have done the heavy lifting already.

In the second post, we developed a generally usable parser to consume TSP problem data in a standard format, and transform it into an adjacency matrix. In the third post, we developed the problem-agnostic BRKGA algorithm.

In this post, we’ll write encoders, decoders and fitness functions to solve a TSP instance with BRKGA, and look at the quality of the solution.

Encoding

We note that the general case we’re solving is for a complete weighted graph. Because the graph is complete, any permutation of node sequences is a Hamiltonian Cycle. Let’s call this permutation a Tour. Note that with TSP problems, the node id’s are 1- based, so we will use the NodeId type for safety.

type Tour = | Tour of NodeId[]

So given a sequence of NodeIds, we need to find an array of floats that encodes the order of the nodes. We do this by generating a bag of sorted random floats. We then map the tour to a chromosome by picking the float that corresponds to the nodeId from the bag. The resultant chromosome will have arbitrary floats as its genes in the traverse order of the tour.

let encodeTSP : Encoder<Tour> =
    let encoder (t : Tour) : Chromosome =
        let cities = match t with Tour x -> x
        let genes =
            [| for _ in 0..(cities.Length - 1) -> rand.NextDouble() |]
            |> Array.sort
        cities
        |> Array.map (fun c -> genes[c.zeroBasedUnapply])
        |> Chromosome.Apply
    encoder

Decoding

Decoding a chromosome to a tour involves finding the node corresponding to each gene’s sorted order. We do that by deducing the sort-order of each gene and taking the node id corresponding to the position.

let decodeTSP : Decoder<Tour> =
    let decoder (chr : Chromosome) =
        chr.Genes
        |> Array.mapi (fun index gene -> (index, gene))
        |> Array.sortBy snd
        |> Array.map (fst >> NodeId.zeroBasedApply)
        |> Tour
    decoder

Computing a tour length uses the adjacency matrix and sums the edges between adjacent cities on the tour, and finally loops back to the start

type WeightedCompleteGraph
with
    member this.TourLength tour =
        let cities = match tour with | Tour x -> x
        let mutable weight = Weight.Zero
        let mutable prev = cities[0]
        for i in 1 .. cities.Length - 1 do
            let curr = cities[i]
            weight <- weight + this[prev, curr]
            prev   <- curr
        weight <- weight + this[cities[cities.Length - 1], cities[0]] // loop back
        weight

Using this, we can create a FitnessFunc:

let fitnessTSP (wcg : WeightedCompleteGraph) : FitnessFunction<Tour> =
    fun (tour : Tour) ->
        (wcg.TourLength tour) <|> (float >> Fitness)

And that’s it. Really. 28 lines of code.

Driver

We’ve encountered the driver before, but I’ll put the entire main function here:

let dataRoot = @"C:\code\TSP\tspsolver\data\tsplib95"
let input =
    [| dataRoot; "att48.tsp" |]
    |> System.IO.Path.Combine
    |> System.IO.File.ReadAllText

option {
    let! wcg = parseTextToWeightedCompleteGraph input
    let pp =
        {
            ChromosomeLength = ChromosomeLength wcg.Dimension.unapply
            InitialPopulationCount = PopulationCount (wcg.Dimension.unapply * 2)
            EncodeFunction = TSPBRKGA.encodeTSP
            DecodeFunction = TSPBRKGA.decodeTSP
            FitnessFunction = TSPBRKGA.fitnessTSP wcg
        }
    let ep = EvolutionParameters.Default
    do UntypedBRKGA.Solve ("TSP") pp ep 20_000
} |> ignore

Not counting the #include lines, the main program is less than 20 lines of code!

Runtime

Running this code results in this console output:

Opening the CSV and plotting Fitness vs RunID gives us:

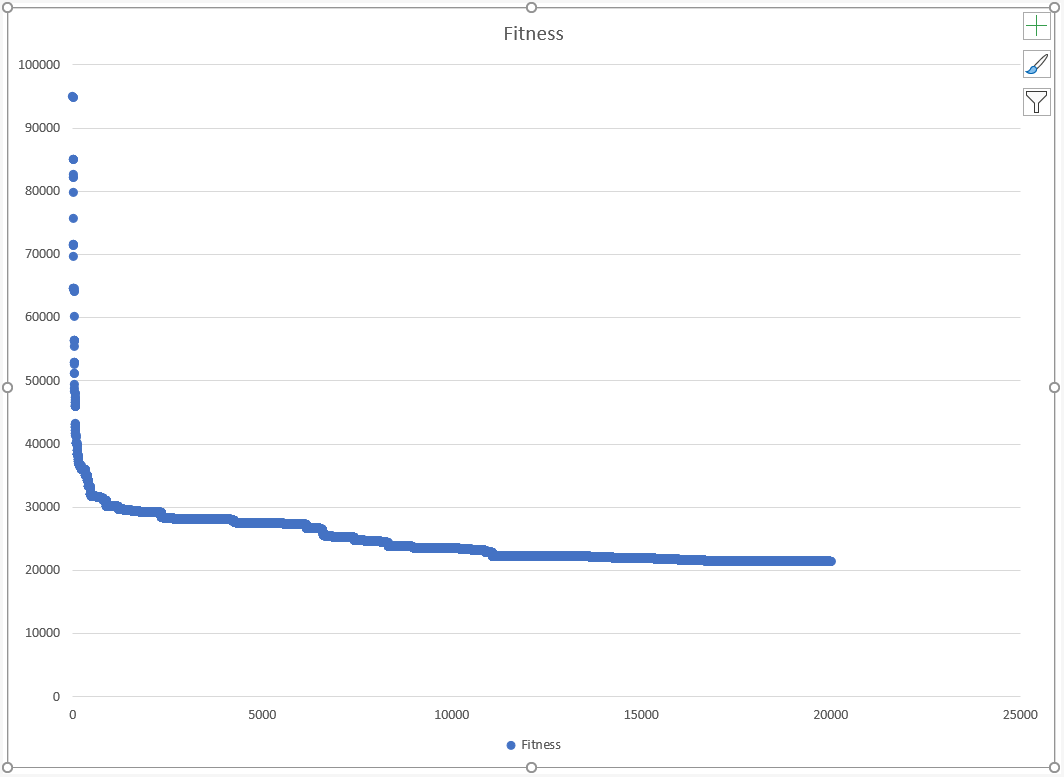
Conclusion

The performance of the BRGKA is impressive - we ran 20,000 iterations in about 5.5s, and saw the tour fitness converge very fast at the beginning, and then plateau off at the end to settle on a path fitness that was only roughly 20% of the path fitness of the starting point.

I’ve seemingly harped on the terse nature of the F# code, but it’s worth pointing out that this terseness has not come at the expense of readability or simplicity of code. That is to say, we haven’t played “code golf” to frivolously try and achieve some terse, unreadable code. I don’t think this feature of F# is rated highly enough!

In the next post, we’ll wrap up this series with a short summary of what we have achieved, and what we can do next!

---

This “Scientific Computing With F#” Series

1. Introduction
2. The Travelling Salesman Problem
3. Biased Random Key Genetic Algorithm
4. Solving TSP with BRKGA
5. Conclusions